Sistem Persamaan Linier Tiga Variabel (SPLTV) Part 2 ~ Sains Seru

Sistem Persamaan Linier Tiga Variabel (SPLTV) Part 2 - Melanjutkan dari materi sebelumnya, kali ini kita akan masuk ke dalam metode yang kedua yaitu metode matriks. Kita ingat sebelumnya telah di bahas materi tentang Sistem Persamaan Linier Tiga Variabel (SPLTV) dengan Metode Subtitusi dan Eliminasi. Sebenarnya untuk menyelesaikan persoalan Persamaan Linier Tiga Variabel (PLTV) menggunakan metode subtitusi dan eliminasi sudah cukup, tetapi ternyata ada metode lain yang lebih mudah dan cepat untuk menyelesaikan persoalan tersebut yaitu metode matriks. Metode matriks ini terbilang lebih efisien dalam menyelesaikan soal Persamaan Linier Tiga Variabel (PLTV). Metode ini lebih di rekomendasikan untuk teman Sains Seru jika mendapatkan soal tersebut dengan waktu yang singkat seperti Ujian Nasional (UN), SBMPTN, dan lain-lain.

Google Image - Sistem Persamaan Linier Tiga Variabel (SPLTV) Part 2

Sistem Persamaan Linier Tiga Variabel (SPLTV) dengan metode matriks ini hasilnya bisa dibuktikan dengan menggunakan metode subtitusi dan eliminasi jika masih kurang yakin. Oke langsung saja kita masuk ke dalam Sistem Persamaan Linier Tiga Variabel (SPLTV) menggunakan metode matriks.

Sistem Persamaan Linier Tiga Variabel (SPLTV) Metode Matriks

Sistem Persamaan Linier Tiga Variabel (SPLTV) menggunakan metode matriks ini sebenarnya salah satu pengembangan dari metode subtitusi dan eliminasi. Seperti yang sudah di jelaskan diatas jika menggunakan metode ini kita akan lebih efisien dalam hal waktu pengerjaannya. Lantas bagaimana cara-cara atau langkah-langkah dalam metode matriks ini.

Bentuk Umum Sistem Persamaan Linier Tiga Variabel (SPLTV)

Secara umum kita harus mengetahui bentuk dari sistem persamaan linier tiga variabel, karena ini adalah modal awal dalam metode matriks. Bentuk umum sistem persamaan linier tiga variabel adalah sebagai berikut.

Nah disini kalian harus mengerti maksud dari gambar diatas. Secara umum a₁, a₂, dan a₃ adalah koefisien dari variabel x. Kemudian b₁, b₂, dan b₃ adalah koefisien dari variabel y. Sedangkan c₁, c₂, dan c₃ adalah koefisien dari variabel z.

Langkah Sistem Persamaan Linier Tiga Variabel (SPLTV) Metode Mariks

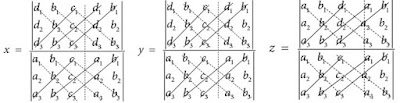
Setelah kita ketahui bentuk umum dari sistem persamaan linier tiga variabel, selanjutnya kita akan masuk ke dalam penyelesaian metode matriks. Bentuk matriks dalam menyelesaikan sistem persamaan linier tiga variabel menggunakan metode matriks adalah sebagai berikut.

Bentuk matriks sistem persamaan linier tiga variabel

Gambar diatas menunjukkan letak-letak angka yang harus ditempatkan ke dalam matriks. Ingat letak mencari nilai dari variabel x, y, dan z berbeda-beda. Jadi teman Sains Seru hanya perlu mengingat letak angka dari bentuk matriks variabel x, y, dan z tersebut.

Cara untuk menghitung nilai matriks diatas yaitu dengan menjumlahkan hasil dari perkalian garis penuh kemudian hasilnya dikurangkan dengan penjumlahan hasil perkalian garis putus putus. Dengan kata lain menghitung nilai x, y, dan z = (penjumlahan hasil perkalian garis penuh) - (penjumlahan hasil perkalian garis putus-putus).

Kemudian kita akan coba menguji apakah metode matriks ini bisa digunakan atau tidak. Untuk mempermudah uji coba metode matriks ini sekarang kita gunakan soal yang sudah pernah digunakan dan diselesaikan menggunkan metode subtitusi eliminasi. Kita akan menggunakan contoh 1 pada artikel sistem persamaan linier tiga variabel part 1, soalnya adalah sebagai berikut.

Contoh 1.

Pak Suprapto memiliki dua hektar sawah yang ditanami padi dan sudah saatnya diberikan pupuk. Ada tiga (3) jenis pupuk yang harus disediakan, yaitu Urea, SS, dan TSP. Ketiga jenis pupuk inilah yang harus digunakan para petani agar hasil panen maksimal. Harga tiap-tiap karung pupuk berturut-turut adalah Rp75.000,00; Rp120.000,00; dan Rp150.000,00. Pak Suprapto membutuhkan sebanyak empat puluh (40) karung untuk sawah yang akan ditanami padi.

Pemakaian pupuk Urea 2 kali banyaknya dari pupuk SS. Sementara dana yang harus disediakan oleh Pak Suprapto untuk membeli pupuk tersebut sebesar Rp4.020.000,00. Berapa karungkah untuk setiap jenis pupuk yang harus dibeli Pak Suprapto?

Jika disajikan dalam persamaan adalah sebagai berikut.

x + y + z = 40

x = 2y

75x + 120y + 150z = 4.020
Carilah nilai x, y, dan z menggunakan metode matriks.

Jawab

Pertama-tama kita tuliskan nilai dari a, b, c, dan dsebagai berikut.
a₁ = 1 b₁ = 1 c₁ = 1 d₁ = 40
a₂ = 1 b₂ = -2 c₂ = 0 d₂ = 0
a₃ = 75 b₃ = 120 c₃ = 150 d₃ = 4.020
Setelah kita ketahui angkanya, kemudian kita masukan angka tersebut ke dalam bentuk matriks sebagai berikut.
mencari nilai x.

mencari nilai y.

mencari nilai z.

Jadi, nilai x, y, dan z secara berturut-turut adalah (22, 11, 7).

Jika kita membandingkan nilai di dapat menggunakan metode matriks ini dengan metode subtitusi eliminasi nilainya ternyata sama, bisa di cek disini hasil contoh 1. Ini membuktikan bahwa metode matriks ini bisa menjadi cara alternatif untuk menyelesaikan persoalan sistem persamaan linier tiga variabel dengan cepat dan tepat.

Kelebihan dan Kekurangan Metode Subtitusi Eliminasi dengan Metode Matriks

Terdapat kelebihan dan kekurangan dari kedua metode yang digunakan, yang pasti semua metode pasti terdapat kelebihan dan kekurangannya bukan. Dibawah ini kita akan berikan kelebihan dan kekurangan dari metode subtitusi eliminasi dengan metode matriks.

Kelebihan
Metode subtitusi eliminasi
1. Tidak terlalu banyak yang di hafal.
2. Perhitungannya simpel.

Metode matriks
1. Waktu pengerjaan akan lebih cepat.
2. Mudah dihitung karena hanya menjumlahkan dari hasil perkalian.

Kekurangan
Metode subtitusi eliminasi
1. Waktu pengerjaan cenderung akan lebih lama.
2. Langkah terbilang panjang sehingga dalam pengecekan ulang terlihat ribet.

Metode matriks
1. Banyak yang harus di hafal.
2. Biasanya rawan dalam perhitungan nilai akhir sehingga sering terjadi salah hitung.

Sistem Persamaan Linier Tiga Variabel (SPLTV) Part 2 - Mungkin itu dulu ya pembahasan singkat ini tentang Sistem Persamaan Linier Tiga Variabel (SPLTV) Metode Matriks. Semoga pembahasan singkat diatas dapat bermanfaat bagi teman setia Sains Seru. Jika ada yang mau ditanyakan bisa tinggalkan di kolom komentar dibawah ya. Untuk pembahasan selanjutnya yaitu Pembahasan Lengkap Soal Sistem Persamaan Linier Tiga Variabel (SPLTV) maka dari itu, ikuti terus update artikel disini ya. Terimakasih atas perhatiannya, See You.