Syarat dan Rumus Fungsi Komposisi serta Contoh Soal - Setelah kita sudah pelajari apa itu fungsi dan aljabar pada fungsi. Pada pertemuan kali ini kita akan melanjutkan materi tantang Fungsi Komposisi. Ternyata fungsi yang telah kita pelajari pada pertemuan sebelumnya bisa di komposisikan, misalnya terdapat fungsi f(x) akan di komposisikan dengan fungsi g(x) sehingga akan membentuk fungsi baru. Dari pernyataan tersebut maka komposisi yang digunakan yaitu fungsi f(x) dan fungsi g(x). Fungsi komposisi ini juga memiliki syarat-syarat yang harus dipenuhi, tidak semua fungsi dapat di komposisikan. Untuk lebih memahami lagi pada pembahasan nanti akan kita berikan juga contoh soal terkait materi tersebut. Baiklah kita langsung saja masuk ke syarat-syarat dari fungsi komposisi.
Syarat dan Aturan Fungsi Komposisi
Seperti yang sudah di jelaskan di atas fungsi dapat di komposisikan dengan memenuhi syarat tertentu. Syarat fungsi g dan f dapat di komposisikan atau g ∘ f ada, jika daerah hasil dari fungsi f adalah himpunan bagian dari daerah asal dari g yaitu f(A) ⊆ Dg.
Jika diketahui himpunan A = {a₁, a₂, a₃}, B = {b₁, b₂, b₃}, dan C = {c₁, c₂, c₃}, maka fungsi f : A → B dan g : B → C seperti ditunjukkan pada gambar berikut.
Dari gambar diatas fungsi A dapat juga langsung di petakan ke C, untuk lebih jelasnya dapat dilihat pada gambar berikut.
Jika fungsi A langsung di petakan ke fungsi C maka fungsi tersebut dianggap fungsi tunggal, gambar diagramnya adalah sebagai berikut.
Fungsi tunggal yang ditunjukkan di atas inilah yang disebut dengan fungsi komposisi. Fungsi komposisi sering dilambangkan dengan g ∘ f dibaca "fungsi g bundaran f". g ∘ f adalah fungsi komposisi yang dimana fungsi f dikerjakan terlebih dahulu dari pada fungsi g. Sedangkan untuk f ∘ g dibaca "fungsi f bundaran g". f ∘ g adalah fungsi komposisi yang dimana fungsi g dikerjakan terlebih dahulu dari pada fungsi f. Secara matematis fungsi komposisi dapat dituliskan sebagai berikut
Agar teman Sains Seru bisa lebih paham lagi, maka kita akan berikan contoh soal, contoh soalnya adalah sebagai berikut.
Contoh soal 1.
Diketahui f(x) = 2x - 1, g(x) = x² + 2.
a. Tentukanlah (g ∘ f)(x)
b. Tentukanlah (f ∘ g)(x)
c. Apakah berlaku sifat komutatif: g ∘ f = f ∘ g.
Jawab
a. (g ∘ f)(x) = g(f(x))
= g(2x - 1)
= (2x - 1)² + 2
= 4x² - 4x + 1 + 2
= 4x² - 4x + 3
b. (f ∘ g)(x) = f(g(x))
= f(x² + 2)
= 2(x² + 2) - 1
= 2x² + 4 - 1
= 2x² + 3
c. Tidak berlaku sifat komutatif karena g ∘ f ≠ f ∘ g.
Contoh soal 2.
Diketahui f(x) = x², g(x) = x - 3, dan h(x) = 5x.
a. Tentukanlah (f ∘ (g ∘ h))(x)
b. Tentukanlah ((f ∘ g) ∘ h)(x)
c. Apakah f ∘ (g ∘ h) = (f ∘ g) ∘ h.
Jawab
a. (g ∘ h)(x) = g(h(x)) = p(x)
= g(5x)
= (5x) - 3
= 5x - 3
(f ∘ (g ∘ h))(x) = f(p(x))
= f(5x - 3)
= (5x - 3)²
= 25x² - 30x + 9
b. (f ∘ g)(x) = f(g(x)) = s(x)
= f(x - 3)
= (x - 3)²
= x² - 6x + 9
((f ∘ g) ∘ h)(x) = s(h(x))
= (5x)² - 6(5x) + 9
= 25x² - 30x + 9
c. Ya, f ∘ (g ∘ h) = (f ∘ g) ∘ h sebab berlaku sifat asosiatif.
Contoh soal 3.
Diketahui f(x) = 5x - 2, I(x) = x.
Buktikan I ∘ f = f ∘ I = f
Jawab
(I ∘ f)(x) = I(f(x))
= I(5x - 2)
= 5x - 2
(f ∘ I)(x) = f(I(x))
= f(x)
= 5(x) - 2
= 5x - 2
Jadi terlihat bahwa I ∘ f = f ∘ I = f (terbukti).
Baca juga:
Relasi dan Fungsi.
Operasi Aljabar Fungsi.
Baca juga:
Nilai Fungsi Komposisi
Setelah kita bisa mencari fungsi dari fungsi komposisi, selanjutnya kita akan mencari nilai dari fungsi komposisi tersebut. Untuk mencari nilai dari fungsi komposisi dapat dilakukan dengan dua cara:
a. Menentukan rumus komposisinya dahlu, kemudian subtitusikan nilainya.
b. Mensubtitusikan secara langsung nilai dari fungsi yang akan dicari.
Mari kita lihat contoh soal biar lebih memahaminya lagi.
Contoh soal 4.
Diketahui fungsi f(x) dan g(x) yang masing-masing rumus fungsinya f(x) = 3x - 1 dan g(x) = x² + 4. Tentukanlah nilai dari fungsi-fungsi komposisi berikut ini.
a. (g ∘ f)(1)
b. (f ∘ g)(-2)
c. (g ∘ f)(-3)
Jawab
Cara pertama
a. (g ∘ f)(x) = g(f(x))
= g(3x - 1)
= (3x - 1)² + 4
= 9x² - 6x + 1 + 4
= 9x² - 6x + 5
(g ∘ f)(1) = 9(1)² - 6(1) + 5
= 9 - 6 + 5
= 8
b. (f ∘ g)(x) = f(g(x))
= f(x² + 4)
= 3(x² + 4) - 1
= 3x² + 12 - 1
= 3x² + 11
(f ∘ g)(-2) = 3(-2)² + 11
= 3(4) + 11
= 23
c. (g ∘ f)(x) = g(f(x))
= 9x² - 6x + 5
(g ∘ f)(-3) = 9(-3)² - 6(-3) + 5
= 9(9) + 18 + 5
= 81 + 18 + 5
= 104
Cara kedua
a. (g ∘ f)(1) = g(f(1))
= g(3(1) - 1)
= g(2)
= (2)² + 4
= 8
b. (f ∘ g)(-2) = f(g(-2))
= f((-2)² + 4)
= f(8)
= 3(8) - 1
= 23
c. (g ∘ f)(-3) = g(f(-3))
= g(3(-3) - 1)
= g(-10)
= (-10)² + 4
= 104
Itulah kedua cara yang bisa digunakan untuk mencari nilai dari fungsi komposisi. Teman Sains Seru bisa memilih cara yang mana yang menurut teman Sains Seru lebih mudah digunakan dan lebih efisien dalam mengerjakan soal.
Syarat dan Rumus Fungsi Komposisi serta Contoh Soal - Demikianlah pembahasan singkat dari Syarat dan Rumus Fungsi Komposisi serta Contoh Soalnya. Semoga pembahasan di atas bisa bermanfaat ya bagi teman setia Sains Seru. Terimakasih sudah bersedia menyimak pembahasan sampai akhir materi ini. Jangan lupa juga untuk selalu mengikuti update artikel disini ya, sampai jumpa di pertemuan selanjutnya. See You.

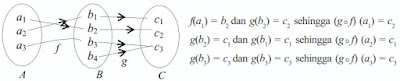


1 comments:
Click here for commentsSyarat ya mana?